关于 硕士阶段的 solver,目前求解器还在修改完善,地址是Aoinzer_Ex。
CFD solver for GRADUATION
1.介绍
对于谷粒干燥这一领域大部分所探讨的数值模型大都是 $single\ kernel$ ,虽然对于求解计算上并无任何不足之处,但是其建立的基础是忽略了固相在干燥过程中对气相的影响。为了研究颗粒干燥过程中其相互影响,因此必须考虑颗粒干燥过程对气相的湿度,温度等物性参数以及其流动状态产生的影响,于是便出于想法尽量对其进行实现。
这里选择OpenFOAM,因为其具有较高的自主性,所以对很适合用于处理气固边界这种复杂类型的问题。下面对根据当前问题所编写的求解器进行一些介绍。
2.整体模型
对于流固之间的热质传递,前人做了很多,但是大都是多孔介质的反应相关,对于干燥蒸发的却少之又少。这里我使用的是MultiRegion方法,其将整个求解模型分成两大部分,一部分是流体,一部分是固体,在计算过程中其分别计算,最终通过其耦合边界进行耦合计算。
2.1气相侧
对于流体域使用的是瞬态的可压缩湍流,在计算中由于几何模型与求解过程的原因可以忽略湍流项,而仅仅使用层流计算。 \(\begin{equation} \frac{\partial \rho_{g}}{\partial t} + \nabla \cdot (\rho_{g}U) = 0 \label{fluid_rhoeqn} \tag{2.1.1} \end{equation}\)
\[\begin{equation} \frac{\partial}{\partial t} ( \rho_{g} U )+\nabla\cdot(\rho_{g}UU )= -\nabla p+\nabla \cdot \tau + \rho_{g} g\label{fluid_ueqn}\tag{2.1.2} \end{equation}\]在上式中其中$eq \ref{fluid_ueqn}$中的$\tau$表述的是总的应力张量(粘性张量和雷诺应力张量),其表述为:
\[\begin{equation} \tau = \mu_{eff}\left[ (\nabla U+ \nabla U^T) - \frac23\nabla\cdot UI \right] \end{equation}\]对于物料运输方程与能量守恒方程为:
\[\begin{equation} \frac{\partial }{\partial t}(\rho_{g}Y_i)+\nabla\cdot(\rho_{g}UY_i) = \nabla\cdot(\rho_{g}D_{eff}\nabla Y_i)\label{fluid_Yeqn}\tag{2.1.3} \end{equation}\] \[\begin{equation} \frac{\partial}{\partial t}(\rho_{g} Uh) + \nabla \cdot (\rho_{g}Uh) +\frac{\partial}{\partial t}(\rho_{g}K_e ) + \nabla\cdot(\rho_{g}UK_e)-\frac{\partial p}{\partial t}=\nabla\cdot(\alpha_{eff}\nabla h)\label{fluid_heqn}\tag{2.1.4} \end{equation}\]对于上述中的各项参数,其中$\rho_{g}$、$p$、$h$分别是气相混合物的密度、压强、与显焓,$U$是速度,$g$是当地的重力加速度,其中$Y_i$表示的是该组分在气相混合物中的质量分数。对于能量$eq\ref{fluid_heqn}$中,$K_e$是气项混合物的动能,而$\alpha_{eff}$是$k/Cp$即热导率与比热容之比,称为等效热扩散系数。而$D_{eff}$称作等效质量扩散系数,又由于本文的研究内容对于米粒的周围的流体流动都是层流,故而上诉的所有相关参数其湍流项与层流项值相同。
2.2固相侧
对于固相,我们认为其与气相为非连续相,且固相在整个模拟计算过程中始终遵循上述的5条假设,在整个计算过程中固相的某些参数会随着温度以及其自身的含水量的变化而变化,因此这里要根据固体的总焓进行能量守恒方程上的计算。
基于之前的假设,对于固体侧,即米粒侧可以推导出其传热守恒方程为:
\[\begin{equation} \rho_{s}Cp_{s}\frac{\partial T}{\partial t} = \nabla(\kappa\cdot\nabla T) + Q_{eva} \label{equation1}\tag{2.2.1} \end{equation}\] \[\begin{equation} \frac{\partial M}{\partial t} = \nabla(D_{eff}\cdot \nabla M) \label{equation2}\tag{2.2.2} \end{equation}\]对于方程$eq\ref{equation1}$,其中$\rho_{s}$是米粒的平均密度$kgm^{-3}$,$Cp_s$为米粒的比热$Jkg^{-1}K^{-1}$,$\kappa$是米粒内部的热导率$Jm^{-1}s^{-1}K^{-1}$,其值随着颗粒内部的含水率的变化而变化,$T$是颗粒的温度$K$,$Q_{eva}$为水分传递到空气中所需要的能量源项。
对于方程$eq\ref{equation2}$,其中$M$为颗粒的含水率,其是一个无量纲数,在本文中其以干基表示为水分的质量与米粒的质量之比,而$D_{eff}$为米粒内部水分的有效扩散系数$m^2s^{-1}$,其值会随着温度的变化而发生变化。
其中对于其特征尺度$d_k(m)$计算为:
\[\begin{equation} d_k = \left( \frac{6V_k}{\pi} \right)^{\frac13} \label{equation3}\tag{2.2.3} \end{equation}\]2.3 初始条件与边界条件
模拟过程中,气相域域固相域是通过其共边界实现耦合计算,在边界上温度可以看作是连续的标量场,而湿度由于存在颗粒的运输效应,且米粒不是多孔介质模型,因此这里是非连续场。
对于温度场,我们认为气相与固相在边界上两侧的温度相同,两侧由于不同的热导率和比热的不同而使得传热状态不同,但是在整个边界上的热通量大小是相同的,且在整个干燥过程,水分蒸发所需要的热量来自于气相传导到固相的能量。因此有在边界上的温度边界条件为:
\[\begin{gather} T_{g} = T_{s}\label{bc_t}\tag{2.3.1}\\ q_{g} = q_{s}\Rightarrow\kappa_{g}\frac{\partial T_{g}}{\partial\vec{n}_{g}}=\kappa_{s}\frac{\partial T_{s}}{\partial\vec{n}_{s}}\label{bc_q}\tag{2.3.2} \end{gather}\]对于湿度的计算,通过分析假设可知,水分迁移是通过在颗粒的表面蒸发,从而损失固相的质量分数,其中水分迁移到空气中,这一部分还决定于空气中的当前质量分数与饱和质量分数,那么有:
\[\begin{equation} \dot{M}_{evp,i} = \rho_{g}H_m(Y_{sat,i}-Y_{g,i})A_{wet,i}\label{evp_rate}\tag{2.3.3} \end{equation}\]对于$\rho_{g}$为气相侧的当前时刻的密度值,$A_{wet,i}$是整个颗粒的表面积,$H_m$这里称作为传质系数,$Y_{sat}$是在饱和状态下的蒸汽的质量分数,同样可以认为其是相对湿度达到1的状态下气相中的水的质量分数,颗粒在整个干燥过程中被空气完全包裹,那么整个颗粒的传质系数可由舍伍德数计算得到,那么有:
\[\begin{gather} Sh = 2 + 0.552Re^{1/2}Sc^{1/3}\label{sh_num}\tag{2.3.4}\\ H_m = \frac{ShD_{eff}}{d_k}\label{hm}\tag{2.3.5}\\ Sc = \frac{\mu_{eff}}{\rho_{g}D_{eff}}\label{Sc}\tag{2.3.6} \end{gather}\]在上式中$Sh$是在气相中的舍伍德数,而$D_{eff}$是气相颗粒表面附近的有效扩散系数,$Re$和$Sc$是气相雷诺数与气相的斯密特数。但是在整个蒸发传质过程的印象因素不单单只是气相中的气相质量分数,还有一部分影响因素是来自于固体米粒表面所能蒸发的水分含量,因此这里引入颗粒平衡含水量来计算固相中的传质量:
\[\begin{gather} \dot{M}_{s,i} = \rho_{s}H_m(Weq-Y_{s,i})A_{wet,i}\label{s_rate}\tag{2.3.7}\\ Weq = \frac 1{14.9306}(ln(\frac{4315.76}{8.32(T_{bc}-91.7849)})-ln(-ln(RH)))\label{Weq}\tag{2.3.8}\\ RH = \frac{p_{evp,i}}{p_{sat}} = \frac{M_{h2o}/M_{comp}p}{p_{sat}}\label{RH}\tag{2.3.9} \end{gather}\]上式中$Weq$为固相在当前温度以及外侧空气相对湿度($RH$)下所能达到的平衡湿度,一般表述为米粒中的结合水与一小部分自由水的质量分数。$M$表示的是在混合物中的该元素的摩尔数,下标$h2o$与$comp$则分别代表着水分的摩尔数与总的摩尔数。那么在传质过程中需要对气相所能获得水分与固相所能蒸发的进行对比,从而决定最终的蒸发量。
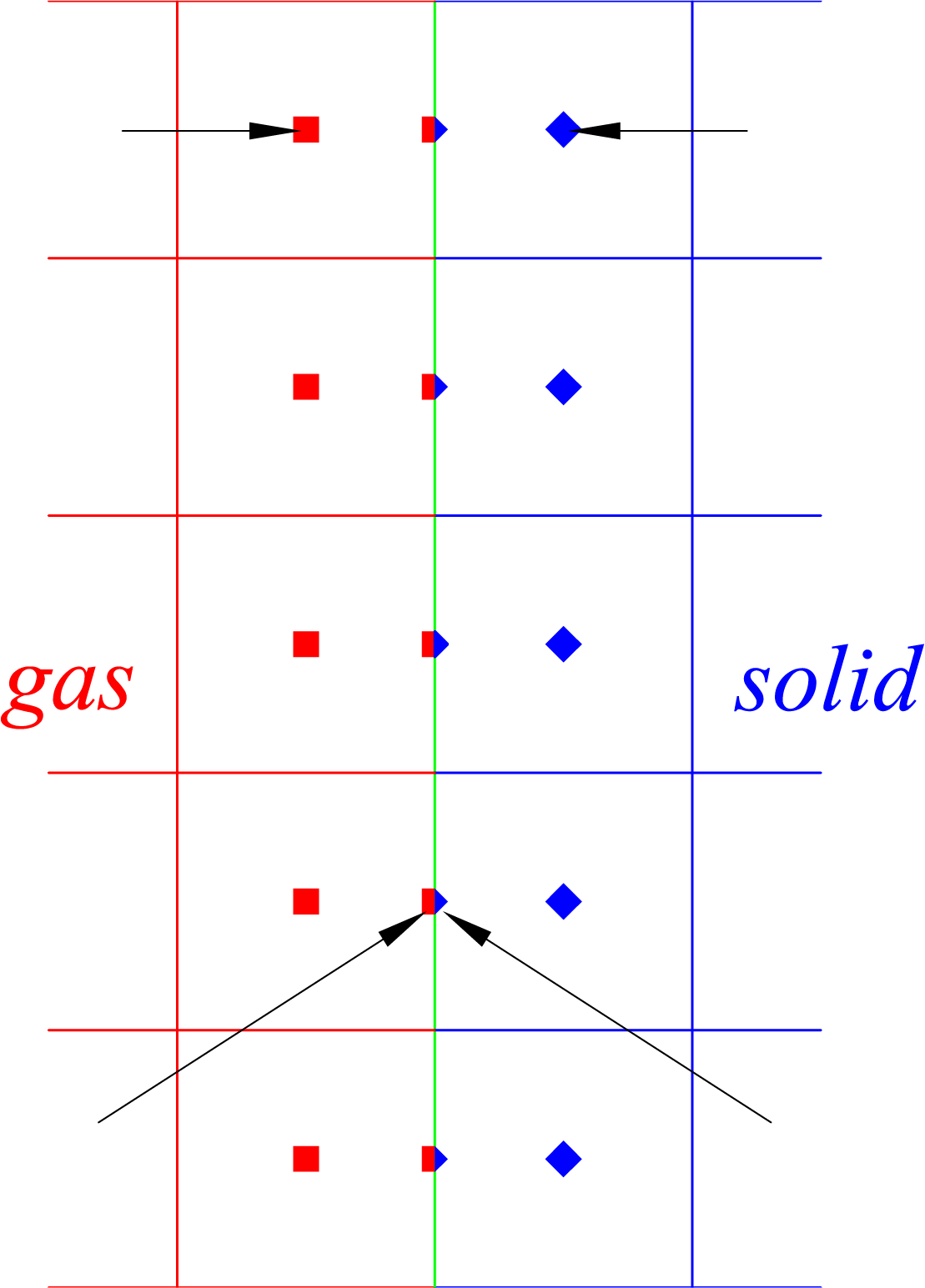
通过边界上的面心的网格的label定义到两侧的耦合网格,再通过气相侧的边界进行计算,将计算出的边界质量通量,通过两侧物理场的密度等分别计算出两侧的边界梯度,实现一种质量的传递,而温度就以OpenFOAM中提供的一种MixedBC进行处理:
对于公式$eq\ref{mixedBC}$中的参数,$\phi$表示的就是某个标量场,其中下标$f$表示边界面上的数据值,而下标$c$表示网格体心中的数据值,下表$ref$表示引用值,对于$\omega$就可以看作是一种在计算过程中产生的权重数据,而$\Delta$这里表示的是边界层网格的面心到体心的距离,那么公式$eq\ref{mixedBC}$就可以看作是一种固定量值的一部分加上扩散通量的一部分,可以类比于第三类(Robin)边界条件。
对于$ref$的选择,为交界面的面心的数据,而其权重的$\omega$的为其两侧的$\kappa \cdot\Delta$的比值,其为$eq\ref{bc_q}$所能获得的一种信息。
2.网格
网格划分选择的是OpenFOAM所提供的snappyHexMesh网格划分工具
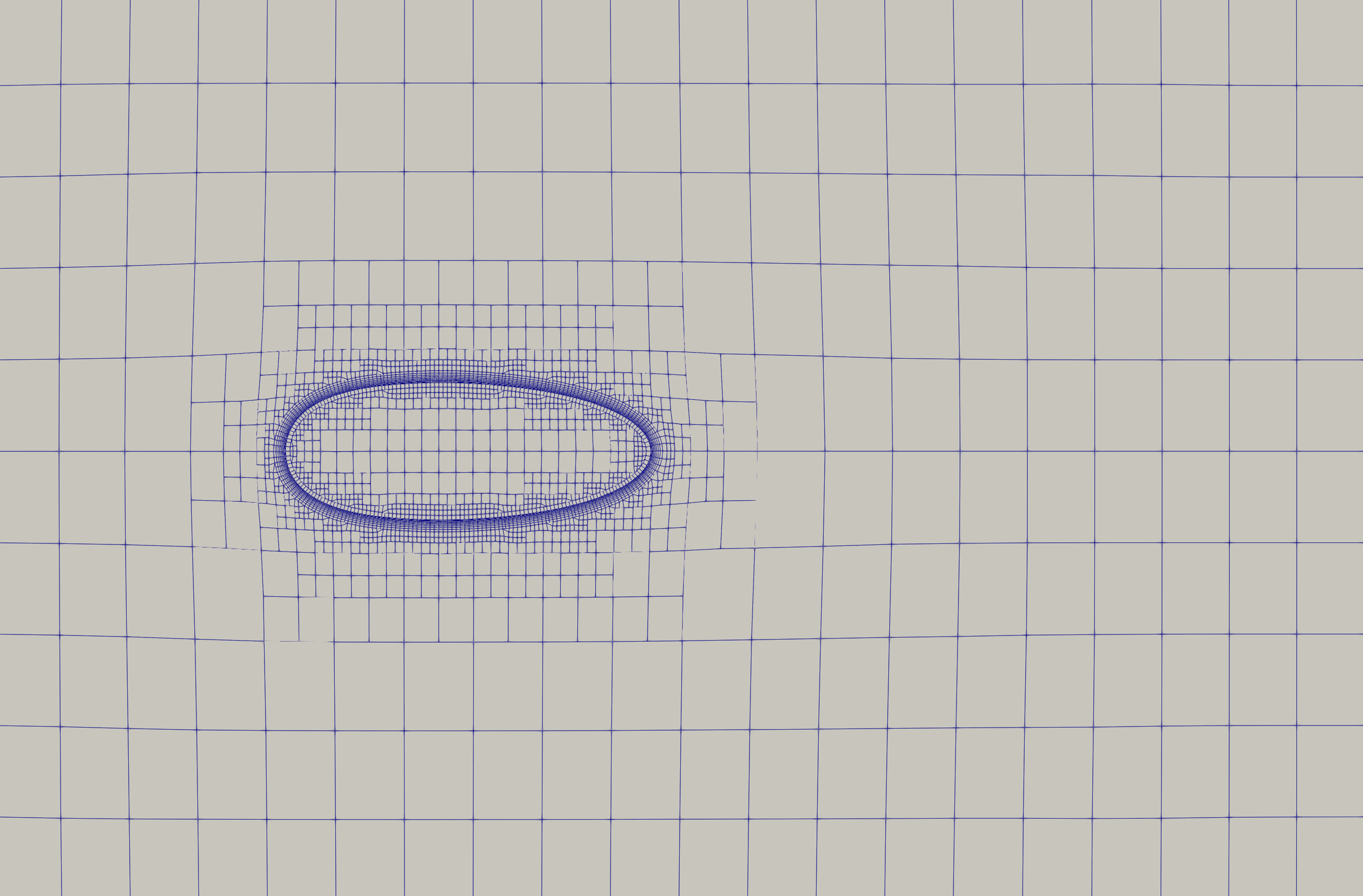
3.计算结果
3.1 平均湿度与平均温度
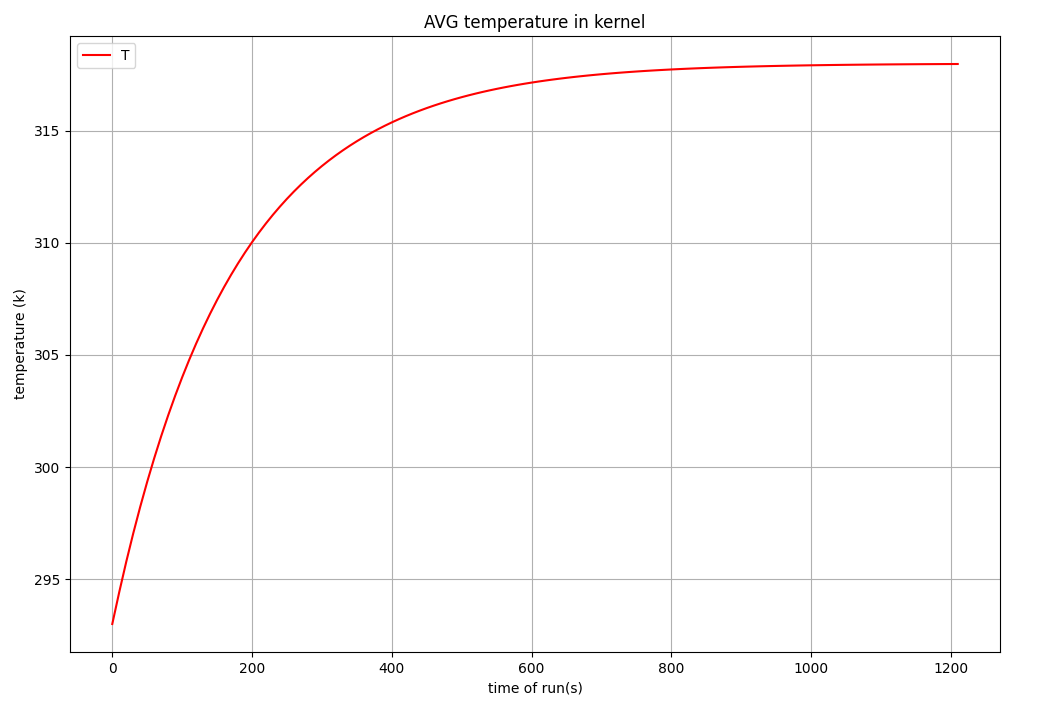
对于其平均湿度与平均温度计算,是通过将每个网格单元的数据配合其网格单元的体积作为权重进行加权求和计算得到的,同理温度的计算是通过焓的总量的形式进行加权求和: \(\begin{equation} M = \frac{\sum^n_i\rho v_iM_i}{\rho v_{tot}} = \frac{\sum^n_i v_iM_i}{v_{tot}}\tag{3.1.1} \end{equation}\) 计算出的温度与湿度的曲线如下:
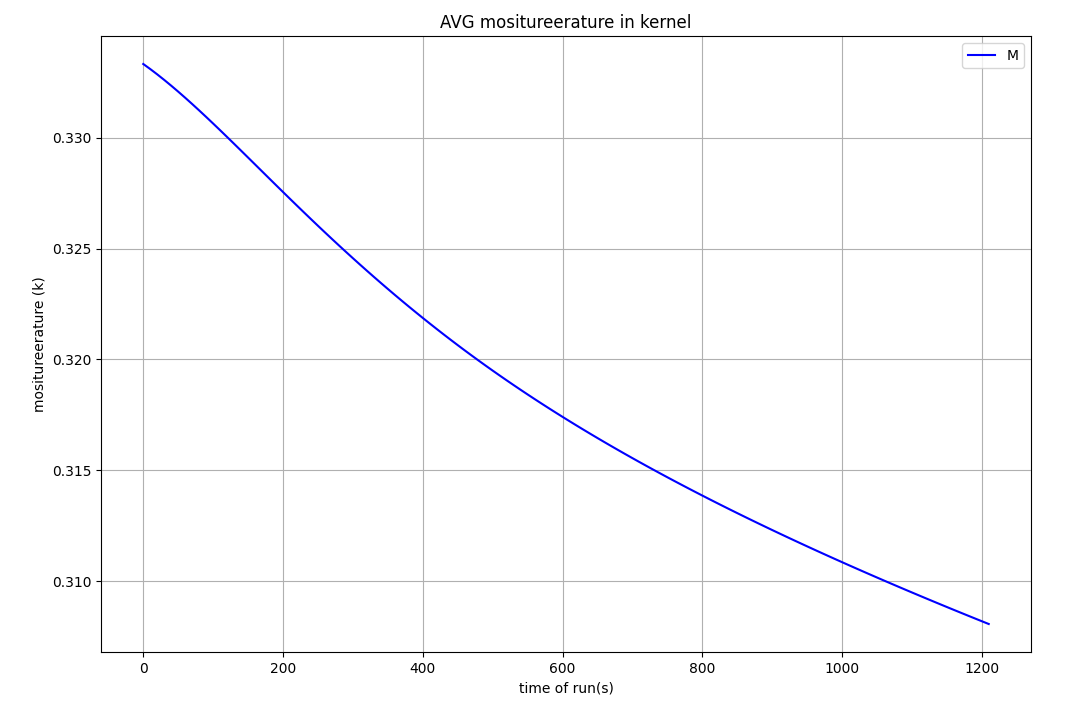
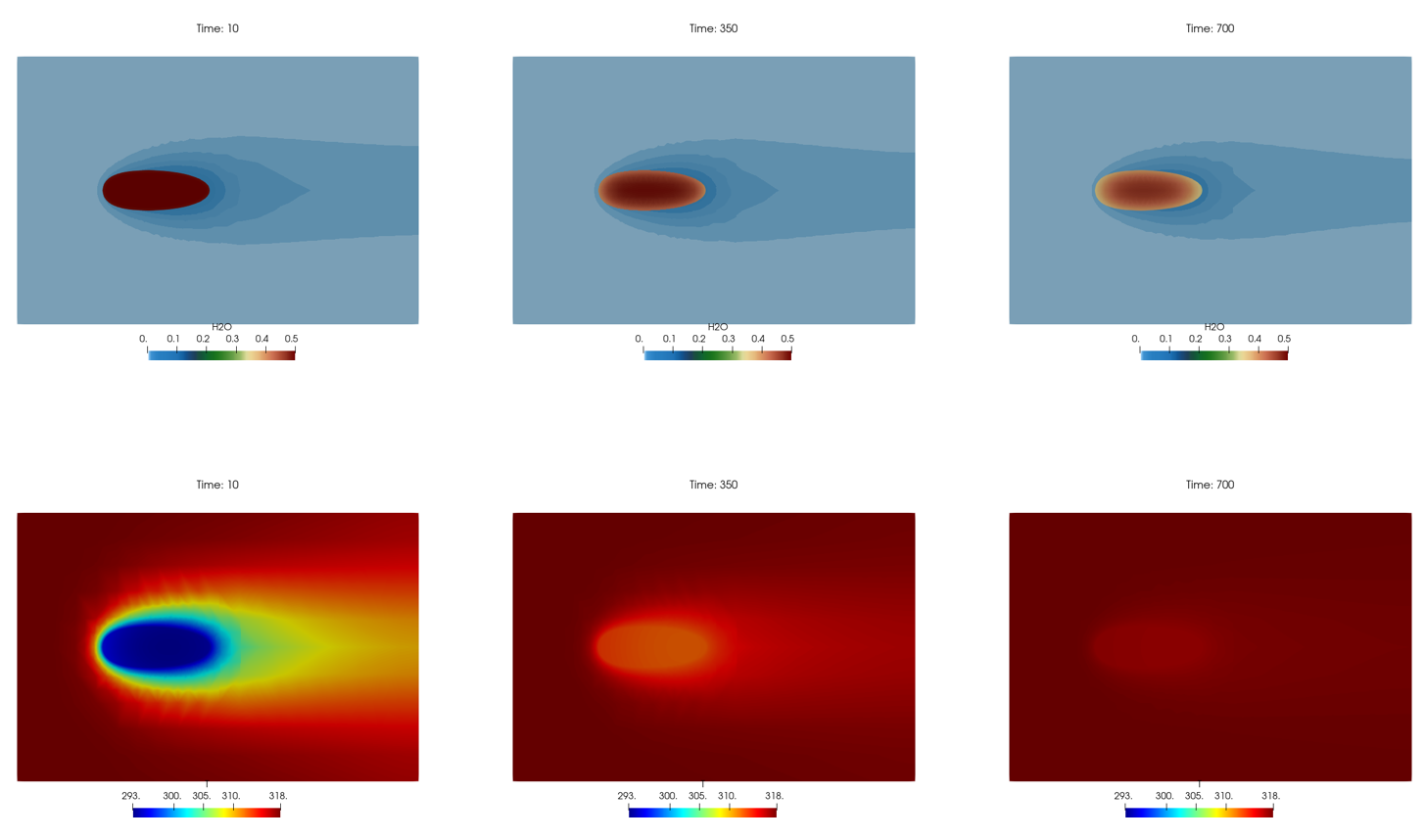
下图为在仿真过程的云图,分别是湿度与温度,时刻分别在10、350、700。