OpenFOAM求解器中的laplacianFoam是求解关于标量场 T 的solver,目前学习编写一个传热传质求解器用以模拟谷粒的传质过程。
基于laplacianFoam的学习汇报
OpenFOAM中laplacianFOAM
在OpenFOAM中的laplacianFOAM是一个求解标量场 $T$ 的求解器,其守恒方程为:
\[\frac{\partial}{\partial t}T - \nabla\cdot(D_T\nabla T)=0\]其中 $D_T$ 为扩散系数,使得方程的量纲平衡,其单位为 $m^2/s$ ,其在case/comstant/transportProperties文件中存在对其的定义。
在整个求解器的控制语句中:
- 时间项为:
fvm::ddt(T) - 梯度项:
fvm::grad(T) - 拉普拉斯项:
fvm::laplacian(DT,T)
那么整个能量守恒方程就写作:
1
fvm::ddt(T) - fvm::laplacian(DT, T) == fvOptions(T)
其中整个laplacianFOAM的求解器场的设置仅有 $T$
1
2
3
4
5
6
7
8
9
10
11
12
volScalarField T
(
IOobject
(
"T",
runTime.timeName(),
mesh,
IOobject::MUST_READ,
IOobject::AUTO_WRITE
),
mesh
);
基于此的kernelFOAM尝试
在传热传质模型中,本质上与laplacianFOAM的守恒方程极为相似,只是添加了一项关于湿度产生的能量迁移:
\[\rho C_p\frac{\partial T}{\partial t}=\nabla\cdot(k\nabla T)+h_g\rho\frac{\partial M}{\partial t}\]其中各个热物理参数单位和其量纲转换分别为:
- $\rho : kg/m^3\qquad\Rightarrow\qquad kg/m^3$
- $C_p : J/(kg\ K)\qquad\Rightarrow\qquad m^2/(s^2\ K)$
- $k: W/(mK)\qquad\Rightarrow\qquad m\ kg/(s^3\ K)$
- $h_g : J/kg\qquad\Rightarrow\qquad m^2/s^2$
- 对于M,其为无量纲数,表示水汽的含量百分比 $(0\sim1)$
对于以上的参数定义全都放置在transportProperties文件内。
但是由于求解器撰写完毕后,testCase过程中量纲计算一直不通过,所以将方程简化了:
\[\frac{\partial T}{\partial t}-\nabla\cdot(k\nabla T)=h\frac{\partial M}{\partial t}\]1
fvm::ddt(T) - fvm::laplacian(k, T) == fvc::ddt(cp,phi)
由于没有撰写关于M的方程,因此这里通过计算单元中的温度变化情况来控制M的变化:
\[\phi^{n+1}=\phi^{n+1}_{temp}-\frac1{600}(T^n-T^{n-1})\phi^n\]在求解器文件中利用一个caculate函数进行计算:
1
2
3
4
5
scalar caculate(scalar t_i,scalar tre_i,scalar phi_i)
{
scalar result = (t_i-tre_i)/600*phi_i;
return result;
}
在求解器的循环内部通过在其运行之时,遍历每个单元进行计算达到M的计算:
1
2
3
4
5
6
7
8
9
if (runTime.time().value()!=0)//非初始时刻
{
Info<<"reading time:"<<runTime.timeName()<<" file!"<<endl;//提示信息
for (label cellI = 0; cellI < mesh.C().size(); cellI++)//遍历全部网格单元
{
phi[cellI] -= caculate(T[cellI],T_re[cellI],phi[cellI]);//计算湿度M受温度变化影响的值
}
}
T_re = T;//将本时刻温度作为下次计算的前一次温度
kernelFOAM测试案例
首先定义了case/constant/transportProperties中的物理参数:
1
2
k k [0 2 -1 0 0 0 0] 4e-05;
cp cp [0 0 -1 1 0 0 0] 1470;
测试算例中使用blockMesh生成个 $0.1\times 0.1(m),20\times20\ cells$ 的一个物理模型。其中上边界为恒温330k,其余均为273k。初始模型phi为0.5。
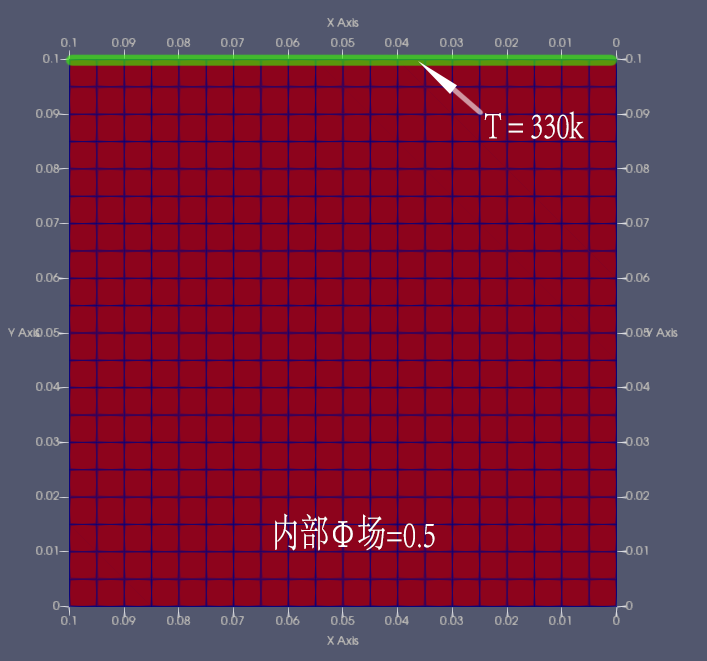
这里我们对模型选取中心一条路径,选取数据点。可以看到在初始时刻,其内部的场的数值和初始设定相吻合。
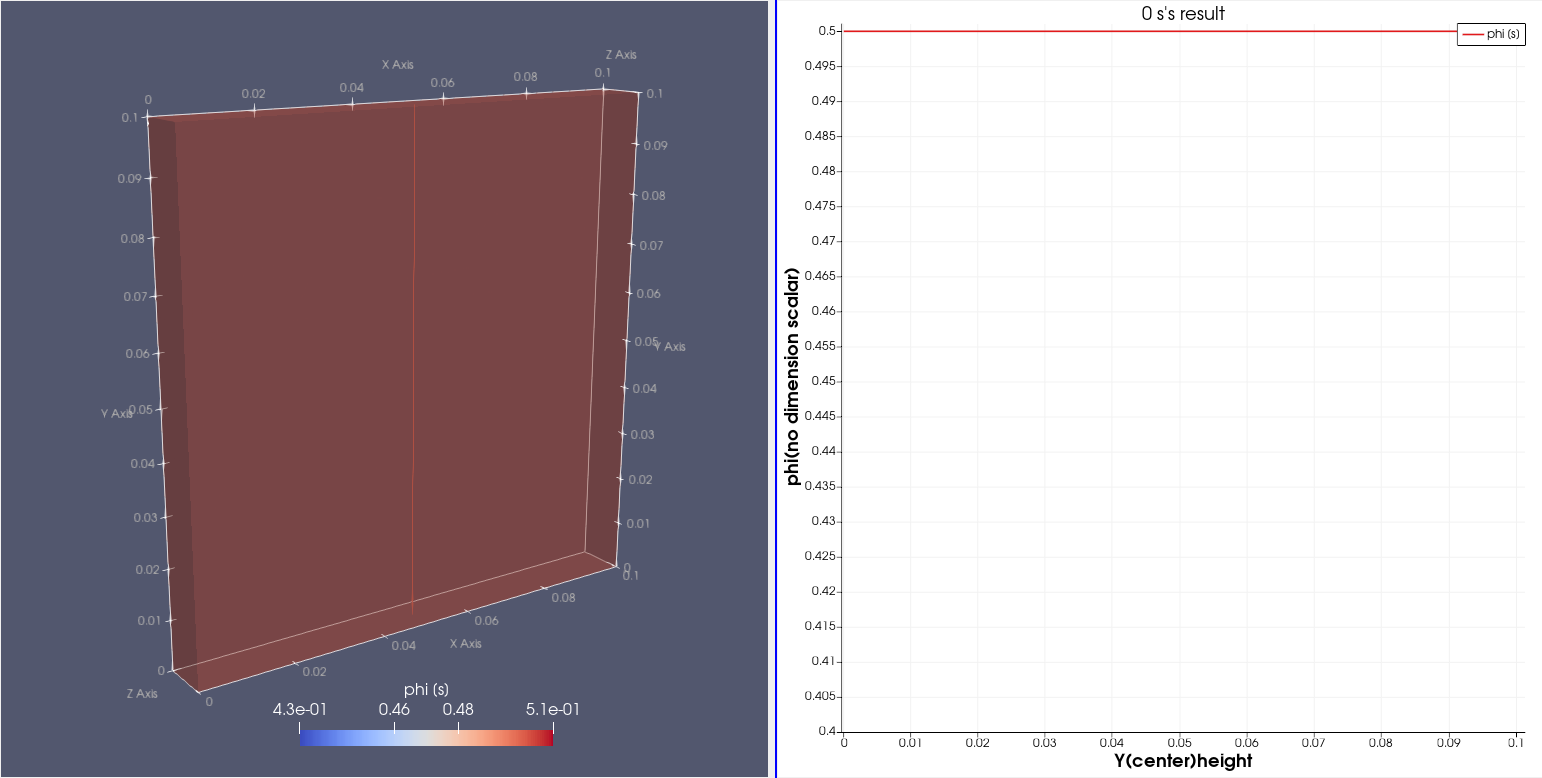
设定fvScheme和fcSolution文件:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
/****************************** fvSchemes ********************************************/
ddtSchemes
{
default bounded backward;
}
gradSchemes
{
default none;
//grad(T) Gauss linear;
}
divSchemes
{
default none;
}
laplacianSchemes
{
default Gauss harmonic uncorrected;
//laplacian(k,T) Gauss linear corrected;
}
interpolationSchemes
{
default none;
}
snGradSchemes
{
default none;
}
/****************************** fvSolution********************************************/
solvers
{
"(T|phi)"
{
solver GAMG;
//preconditioner DIC;
tolerance 1e-06;
smoother symGaussSeidel;
relTol 0;
}
}
SIMPLE
{
nNonOrthogonalCorrectors 2;
}
PIMPLE
{
nOuterCorrectors 20;
outerCorrectorResidualControl
{
T
{
relTol 0;
tolerance 1e-6;
}
phi
{
relTol 0;
tolerance 1e-6;
}
}
}
relaxationFactors
{
equations
{
T 1;
phi 1;
}
}
这里的设定与laplacianFOAM中的基本大差不差。
计算的时间步长取0.005,总的计算时间为1,并限制phi的范围为 $0\sim1$ 。
在终端中输入:blockMesh kernelTransportFoam后等待求解完成。
首先对于温度场的变化:
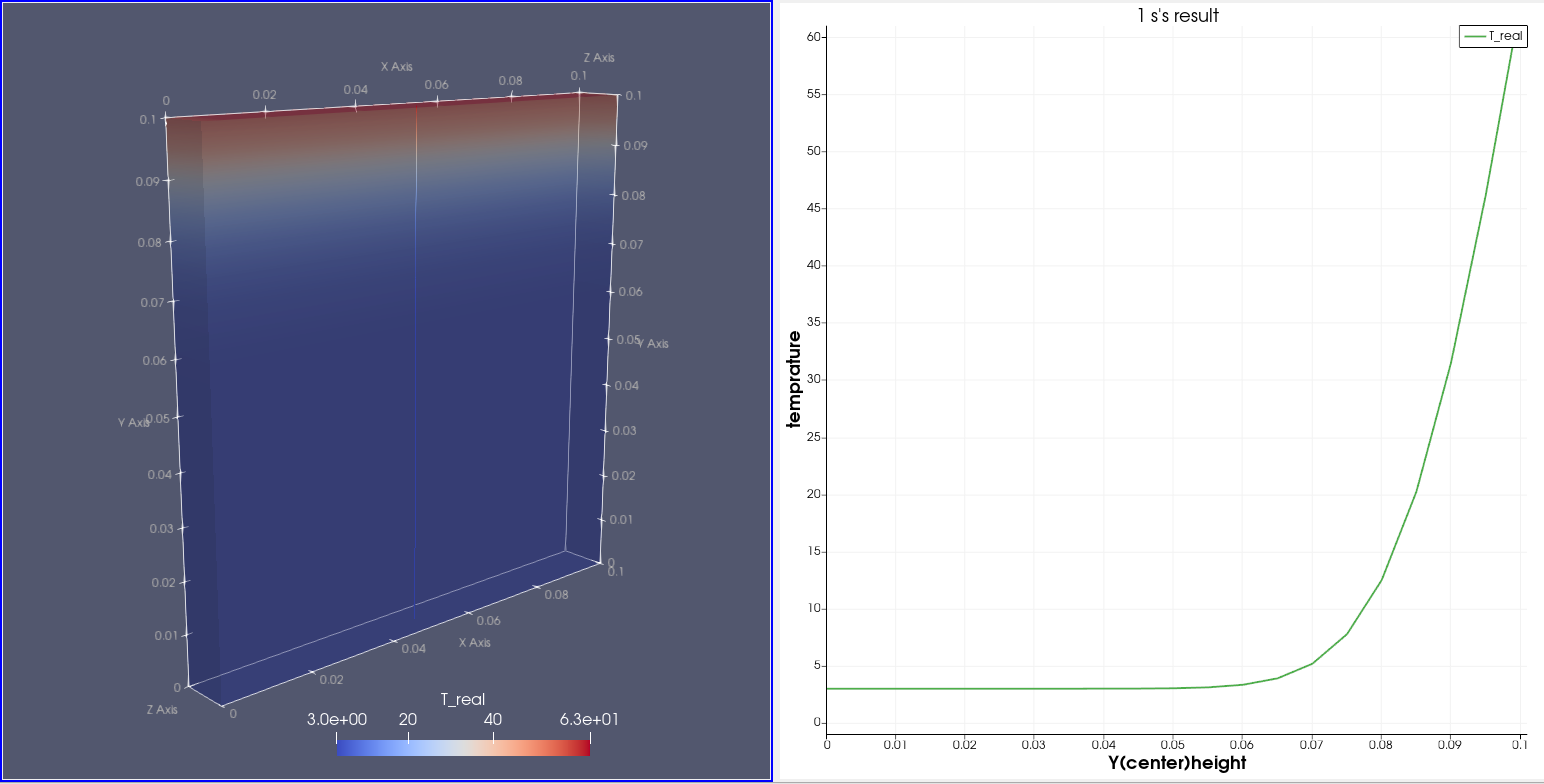
可以看到温度随着传热的发生,模型的内部温度场也在缓慢的升温。
再看一下湿度phi随温度的变化情况:
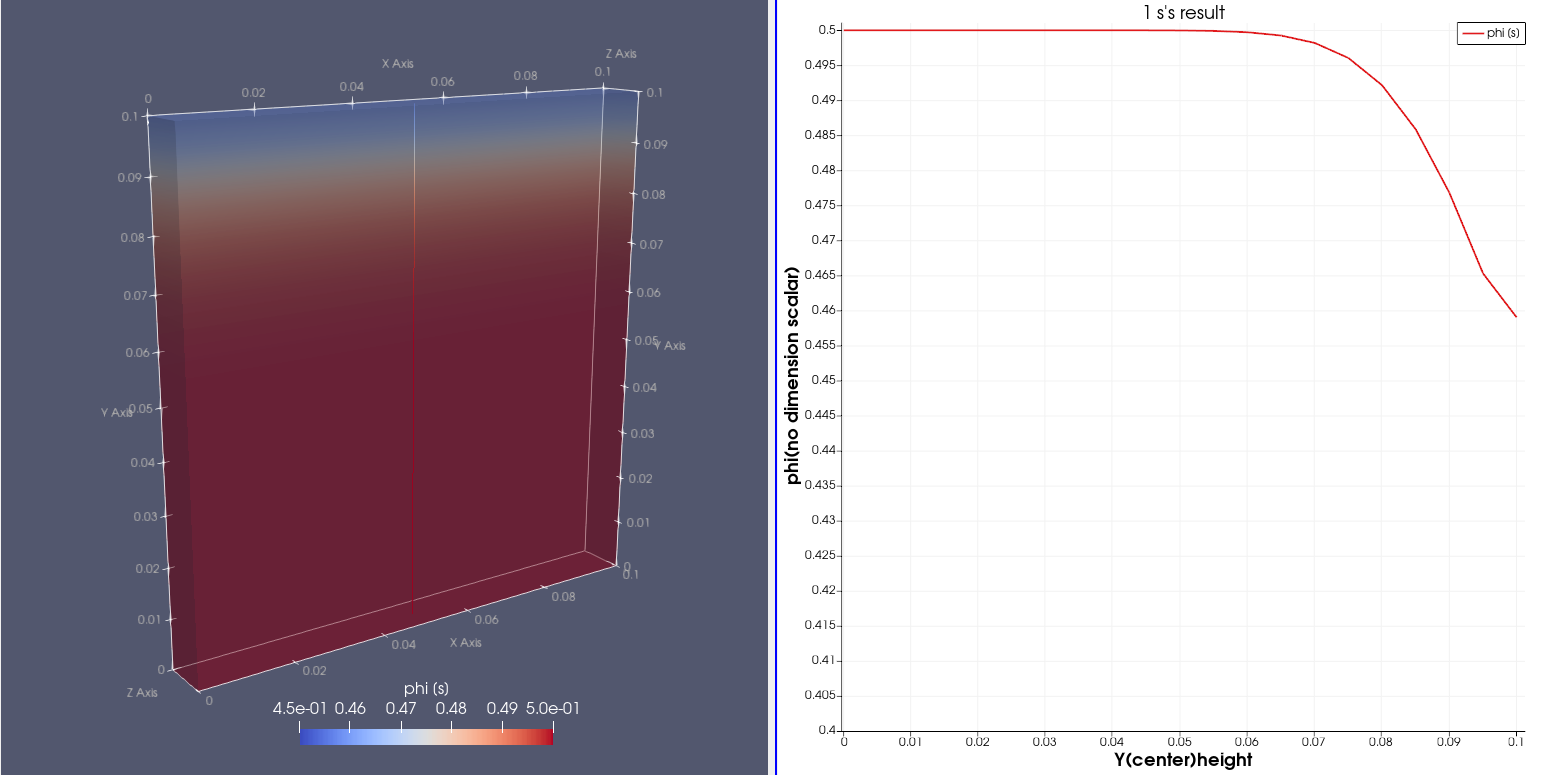
可以看出随着温度的逐渐升高,单元中的湿度随着温度的升高而下降,切曲线的变化趋势和之前在solver文件中设定的基本一样。
总结
这只是我在学习OpenFOAM过程中的一步,仅仅只是作为学习记录,内容难免会出现错误,希望大家能相互交流学习进步。