多区域计算方法的耦合边界条件解读

关于OpenFOAM 中 chtMultiRegionFOAM 的 case 中的边界处理解读

---

多区域计算方法的耦合边界条件解读

1. compressible::turbulentTemperatureCoupledBaffleMixed

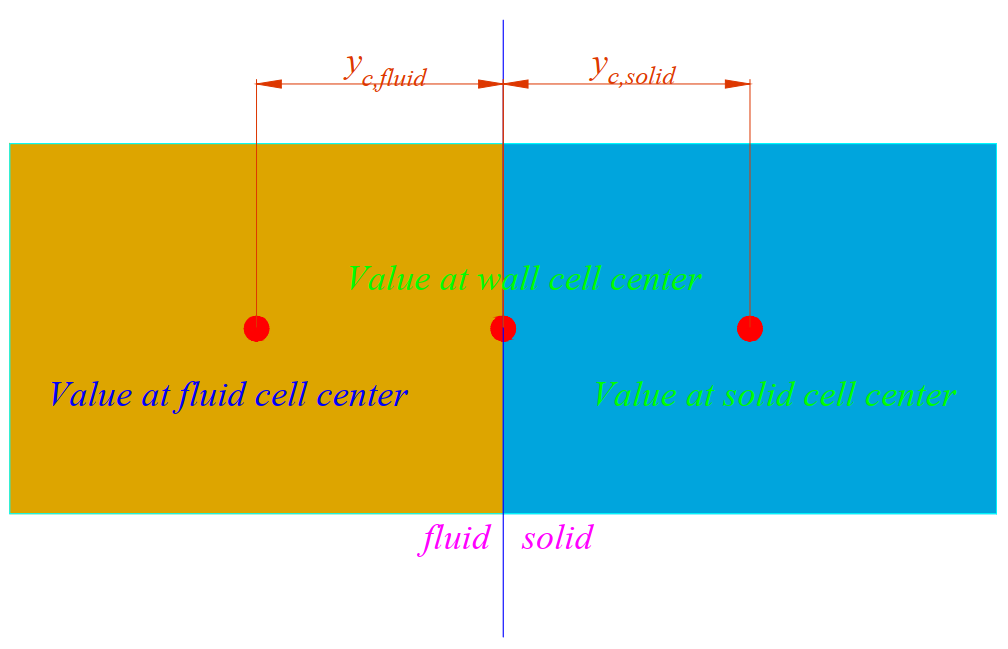
对于此耦合边界传热计算，其不是通过对流传热理论来计算的，之前在很多帖子上发现有人误解了其计算依据。简单的来说其主要是通过满足了以下等式： \(\begin{align} Q_s & = -Q_f\\ T_{ps} & = T_{pf} \end{align}\)

这里的表述含义就是，对于两侧区域，其在mappedPatch上的面心温度一致，且两侧的热通量相同！那么照此梳理就很简单了。

对上式展开，可以看出：

\[\begin{align} &Q_s &=\qquad -&Q_f\\ &\Downarrow & &\Downarrow\\ k_s&\nabla T_s &-k_f&\nabla T_f \end{align}\]

对两侧 $\nabla T$ 进行展开，可以得到整式：

\[\begin{align} k_s\Delta_s(T_s-T_{ps}) &= -k_f\Delta_f(T_f-T_{pf})\\ \Delta = \frac 1\delta \quad&\quad T_{ps} = T_{pf}\\ \Downarrow\\ T_p = \frac{k_s\Delta_s}{k_s\Delta_s + k_f\Delta_f}T_s & +\frac{k_f\Delta_f}{k_s\Delta_s + k_f\Delta_f}T_f \end{align}\]

对于turbulentTemperatureCoupledBaffleMixedFvPatchScalarField.C中的updateCoeffs()

有如下的赋值计算：

this->refValue() = nbrIntFld();
this->refGrad() = 0.0;
this->valueFraction() = nbrKDelta()/(nbrKDelta() + myKDelta());

对于 OpenFOAM 其定义了这么一种 Mixed 模式：

\[\phi_p = \omega\phi_{ref}+(1-\omega)(\phi_c+\Delta\nabla{\phi_{ref}})\]

那么将上面推导的等式转换到 Mixed 模式，如果当前计算域是流体$(fluid)$侧，有：

\[\begin{align} \nabla\phi_{ref} &= 0\\ \phi_{ref} &= T_s\\ \phi_c &= T_f \\ \omega &= \frac{k_s\Delta_s}{k_s\Delta_s + k_f\Delta_f} \end{align}\]

对于代码部分，通过阅读源码上下内容，可知：

KDelta = kappa() * patch().deltaCoeffs();
//kappa就是k，deltaCoeffs是体心到patch面心距离的倒数。即上面 Δ ;

2. humidityTemperatureCoupledMixed

对于这里我们只看冷凝无辐射状态下的多域耦合计算的边界处理，对于此边界，其基本理论与上述内容一致，只是其添加了介质的体积热与潜热部分，且介质在区域接触存在串联热阻！对此可以知道，其满足如下的等式：

\[\begin{align} Q_s & = -Q_f - Q_w\\ T_{ps} & = T_{pf} \end{align}\]

对于其中的各个 $Qflux$ 有如下的关系：

\[\begin{align} Q_s & = k_s\nabla T_s = k_s\Delta_s(T_s- T_{ps})\\ Q_f & = k_f\nabla T_f = \frac{T_f - T_{pf}}{\sum R_t} = \frac 1{\frac 1{k_f\Delta_f}+\frac 1{h_t}}(T_f - T_{pf})\\ Q_w & = \dot mH_{fg}+mC_p(T_p - T_f^{old}) \end{align}\]

对于上述的内容中，$ht$表示的是冷凝水在当前的温度状态下的换热系数，$\dot m$是当前时刻的冷凝的质量速率，$m$是总的冷凝的水分为$\sum_t \dot mdt$，$T_f^{old}$表示的是上一个时刻下的网格温度。那么这里的$Q_w$就是相变能量与总的冷凝水的体积热。

通过如 turbulentTemperatureCoupled中的推导一样，可以得到如下的关系式：

\[\left(\frac 1{\frac 1{k_f\Delta_f}+\frac 1{h_t}}+k_s\Delta_s + mC_p\right) T_p=\frac 1{\frac 1{k_f\Delta_f}+\frac 1{h_t}}T_f-k_s\Delta_sT_s-mC_pT_f^{old}-\dot mH_{fg}\]

那么将其转换为 mixed 的表达形式，可以有：

\[T_p= \frac{\frac 1{\frac 1{k_f\Delta_f}+\frac 1{h_t}}}{\frac 1{\frac 1{k_f\Delta_f}+\frac 1{h_t}}+k_s\Delta_s + mC_p}T_f - \frac{k_s\Delta_sT_s -mC_pT_f^{old}-\dot mH_{fg}}{\frac 1{\frac 1{k_f\Delta_f}+\frac 1{h_t}}+k_s\Delta_s + mC_p}\]

其中各个系数推导为：

\[\begin{align} \phi_f & = T_p\\ \phi_c & = T_c\\ \alpha & = k_s\Delta_s + mC_p\\ \omega & = \frac{\alpha}{\frac 1{\frac 1{k_f\Delta_f}+\frac 1{h_t}}+\alpha}\\ \phi_{ref} & = \frac{k_s\Delta_sT_s -mC_pT_f^{old}-\dot mH_{fg}}{\alpha} \end{align}\]

在该边界条件的源代码中，可以看到：

//in this patch constructor we can see :
{
    ...
    refGrad() = 0.0;
	...
}
//... if in fluid side
//kfΔf
myKDelta_ = this->kappa(*this)*patch().deltaCoeffs();
//ksΔs
KDeltaNbr(nbrField.kappa(*this)*nbrPatch.deltaCoeffs());
//dm calculate
dm = -rhof*hm*max((Ys - Yinf), 0.0)/(1.0 - Ys);
// Total mass accumulated [Kg]
mass_ += dm*magSf*dt;
//resistance in condensation
htc = htcCondensation(TSat, Re)*nbrK/L_;
//total heat resistance
myKDelta_ = 1.0/((1.0/myKDelta_) + (1.0/htc));
// volume heat capacity
mpCpTp_ = mass_*cp/dt/magSf;
// Heat flux due to change of phase [W/m2]
dmHfg_ = dm*hfg;
scalarField mpCpTpNbr(patch().size(), Zero);
scalarField dmHfgNbr(patch().size(), Zero);
const scalarField dmHfg(dmHfgNbr + dmHfg_);
const scalarField mpCpdt(mpCpTpNbr + mpCpTp_);
// qr = 0 in this note
scalarField alpha(KDeltaNbr + mpCpdt - (qr + qrNbr)/Tp);
valueFraction() = alpha/(alpha + myKDelta_);
refValue() = (KDeltaNbr*nbrIntFld + mpCpdt*TpOld + dmHfg)/alpha;

总结

对于多区域的标量传递基本都是通过下式计算，关键就是源项的处理如何添加。但是对于多区域方法计算，当遇到复杂的两侧场发生交互的情况下，处理方式将会变得非常棘手，所以多区域的处理并不是一定就能适合非连续性介质的计算。

\[\begin{align} Q_1 & = -Q_2\\ T_{p1} & = T_{p2} \end{align}\]

本人水平不足，如有错误欢迎指出——Aoinzer_Ex